What is Linear Convolution and properties of linear convolution
Linear Convolution
Linear convolution is a mathematical operation done to calculate the output of any Linear-Time Invariant (LTI) system given its input and impulse response. It is applicable for both continuous and discrete-time signals.
We can represent Linear Convolution as
y(n)=x(n)*h(n)
Here, y(n) is the output (also known as convolution sum). x(n) is the input signal, and h(n) is the impulse response of the LTI system.
In linear convolution, both the sequences (input and impulse response) may or may not be of equal sizes. That is, they may or may not have the same number of samples. Thus the output, too, may or may not have the same number of samples as any of the inputs.
For example:-
consider the following signals
x(n): [1,2,3]
h(n): [1,2,3,4,5]
As you can see, the number of samples in the input and Impulse response signals is not the same. Still, linear convolution is possible.
Here’s how you calculate the number of samples in the output of linear convolution.
L = M + N – 1
Where M is the number of samples in x(n). N is the number of samples in h(n).
For the above example, the output will have (3+5-1) = 7 samples.
Graphically, when we perform linear convolution, there is a linear shift taking place. Check out the formula for a convolution.
∞
Σ x(k)h(n-k)
-∞
There is a folding of the IR sequence, shifting it by n, multiplying it with another sequence (input), and summing the resulting products.
It is possible to find the response of a filter using linear convolution. Linear convolution may or may not result in a periodic output signal.
What are the properties of linear convolution?
Linear convolution has three important properties- Commutative property
- Associative property
- Distributive property
Commutative property of linear convolution
This property states that linear convolution is a commutative operation. A sample equation would do a better job of explaining the commutative property than any explanation.x(n)*h(n) = h(n)*x(n)
Associative property of linear convolution
According to the associative property of convolution, we can replace a cascade of Linear-Time Invariant systems in series by a single system whose impulse response is equal to the convolution of the impulse responses of the individual LTI systems.y(n) = [x(n)*h1(n)]*h2(n) = x(n)*[h1(n)*h2(n)]
Graphically, the associative property of convolution can be represented, as shown below.
Distributive property of linear convolution
The distributive property of linear convolution applies to ‘distributed’ systems. Meaning, if we have two individual Linear-Time Invariant systems with their own individual impulses responses, we can combine them. We can merge them into one LTI system whose impulse response is equal to the sum of the individual responses of the constituent systems. This equation will clear things up a bit.x(n)*[h1(n)+h2(n)] = [x(n)*h1(n)]+[x(n)*h2(n)]
Graphically this can be represented as shown below.
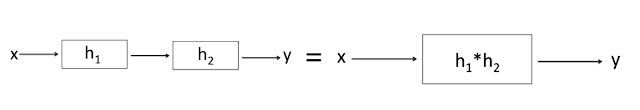

Comments
Post a Comment